Vor mittlerweile über einem Jahr arbeitete ich relativ intensiv an einer Arbeit im Bereich der Topologischen Datenanalyse (TDA). Als Nicht-Vollblut-Mathematiker (sondern Informatiker) ist der Einstieg in dieses Themengebiet nicht unbedingt der Einfachste. Im Rahmen der Arbeit entstand deshalb eine relativ großzügige Literaturliste. Neben rund 100 Quellen, die detailliert im Themengebiet beheimatet sind, war selbstverständlich auch Einstiegsliteratur enthalten. Bisher fand ich nicht die Zeit, diese Liste zu veröffentlichen. Ich bin mir allerdings sicher, dass die Literaturempfehlungen der ein oder anderen Person zumindest etwas Zeit sparen könnte, weshalb ich meine Empfehlungen für den Einstieg in den Themenbereich unten präsentiere. Die vollständige Literaturliste mit rund 100 Quellen werde ich in einem separaten Beitrag online stellen.
Vorwarnung: Diese Liste richtet sich daher vermutlich eher nicht an Mathematiker. Diese dürften mit den entsprechenden Grundlagen bereits vertraut sein. Viel mehr dient sie Praktikern und Anwendern aus anderen Bereichen, die mit Topologie und Topologischer Datenanalyse bislang wenig zu tun hatten.
Grundidee der Topologie und Topologischen Datenanalyse
Ohne groß in Details einzutauchen, möchte ich an dieser Stelle kurz und bündig die Idee hinter der TDA zusammenfassen. An dieser Stelle bereits ein Hinweis auf das "Landscape-Paper" von Gunnar Carlsson, das im Wesentlichen den Grundstein für jegliche weitere Forschung in diesem Bereich legte: Topology and Data. Die Topologie und damit die Topologische Datenanalyse dreht sich gewissermaßen um die qualitativen Eigenschaften eines Objekts. Sie beschäftigt sich mit den Eigenschaften eines Objekts, die unter sog. kontinuierlichen Deformationen gleich bleiben. Das klingt kompliziert, ist aber (vereinfacht) eigentlich ziemlich schnell erklärt: Solange zwei Objekte durch Stauchen, Dehnen, Drehen und Falten ineinander überführt werden können, so werden sie in der Topologie als gleich angesehen. Ein klassisches Beispiel: Ein Donut und eine Kaffeetasse. Die Topologie sieht beide Objekte als gleich an. Denn den Donut könnte man durch etwas Dehnen auf einer Seite etwas aufblähen - schon hätte man die Grundform einer Kaffeetasse (großer Korpus links, ein kleiner Henkel rechts). Jetzt noch mit einer Faust ein Loch von oben hinein gedrückt - und schon ist die Tasse auch tatsächlich eine Tasse. Eine kontinuierliche Transformation also. Man könnte auch sagen: Beide Objekte bestehen aus einem zusammenhängenden Korpus und besitzen ein einziges Loch.

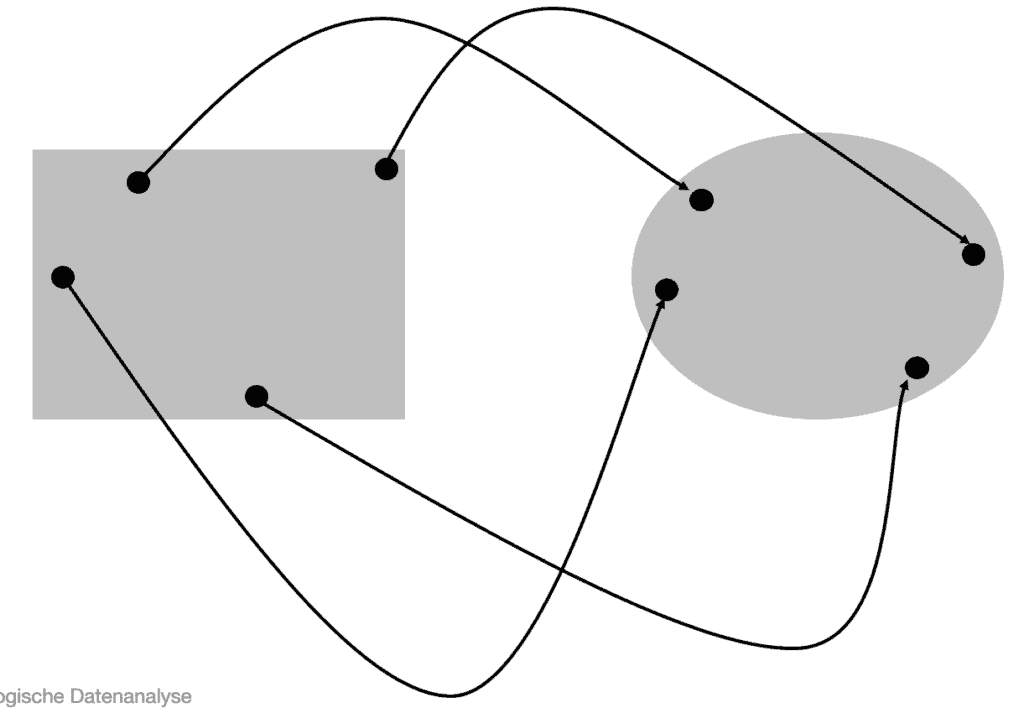
Genauso sind übrigens auch ein (gefülltes) Rechteck und ein (gefüllter) Kreis unter topologischen Gesichtspunkten gleich, also homöomorph - beide Objekte bestehen aus einem zusammenhängenden Korpus und haben keinerlei Löcher. Es handelt sich um eine sogenannte "bijektive Abbildung".
Allerdings soll dieser Blogbeitrag natürlich keine eigene, allumfassende Einführung in die TDA werden. So viel sei aber an dieser Stelle gesagt: Die Topologische Datenanalyse kann Daten (etwa mehrdimensionale Rohdaten) aufgrund ihrer qualitativen Eigenschaften vergleichen - und so beispielsweise für ähnlich befinden. Ein dafür spannendes Konzept ist die persistente Homologie (persistent Homolog), die eine sehr große Rolle spielt. Sie erlaubt eben diesen qualitativen Vergleich und wird in einer ganzen Reihe an Quellen detaillierter behandelt.
Mathematische Grundlagen
Zum Verständnis der notwendigen mathematischen Grundlagen fand ich folgende Quellen besonders hilfreich:
| Ghrist (2014) | Elementary Applied Topology |
| Morris | Topology without tears |
| Waldmann (2014) | Topology: An introduction |
| Sato (1996) | Algebraic topology - An intuitive approach |
| Hatcher (2002) | Algebraic Topology |
| Prasolov (1994) | Intuitive Topology |
| Munkres (2002) | Topology |
| Tokieda (2014) | Topology & Geometry |
Persistente Homologie
Die Topologische Datenanlyse baut zu großen Teilen auf der "persistenten Homologie" auf. Hier sind folgende Quellen in meinen Augen besonders hilfreich:
| Mapper-Algorithmus | Singh, Mémoli, Carlsson (2007) | Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition |
| Persistent Homology | Edelsbrunner, Letscher, Zomorodian (2002) | Topological Persistence and Simplification |
| Persistent Homology | Edelsbrunner, Harer (2008) | Persistent Homology – a Survey |
| Persistent Homology, Barcodes | Grhrist (2008) | Barcodes: The persistent topology of data |
| Persistent Homology, Barcodes | Zomorodian, Carlsson (2005) | Computing Persistent Homology |
| Persistent Homology, Persistence Diagrams | Cohen-Steiner, Edelsbrunner, Harer (2007) | Stability of Persistence Diagrams |
| Simplicial Complexes | de Silva, Carlsson (2004) | Topological estimation using witness complexes |
| Persistent Homology | Fugacci, Scaramuccia, Iuricich, De Floriani (2016) | Persistent homology: a step-by-step introduction for newcomers |
Topologische Datenanalyse
Gute Einführungen in den konkreten Bereich der Topologischen Datenanlyse bieten meines Erachtens folgende Quellen:
| Biology, Chemistry | Offroy, Duponchel (2015) | Topological data analysis: A promising big data exploration tool in biology, analytical chemistry and physical chemistry |
| General | Munch (2017) | A User's Guide to Topological Data Analysis |
| General | Tierny (2017) | Introduction to Topological Data Analysis |
| General | Chazal, Michel (2017) | An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists |
| General | Lum, Singh, Lehman, Ishkanov, Vejdemo-Johansson, Alagappan, Carlsson J., Carlsson G. (2013) | Extracting insights from the shape of complex data using topology |
| Statistics | Medina, Doerge (2016) | Statistical Methods in Topological Data Analysis for Complex, High-Dimensional Data |
| Tutorial, Implementation | Otter, Porter, Tillmann, Grindrod, Harrington (2017) | A roadmap for the computation of persistent homology |
| General | Wasserman (2018) | Topological Data Analysis |